20 June 2007
Mapping the Internet
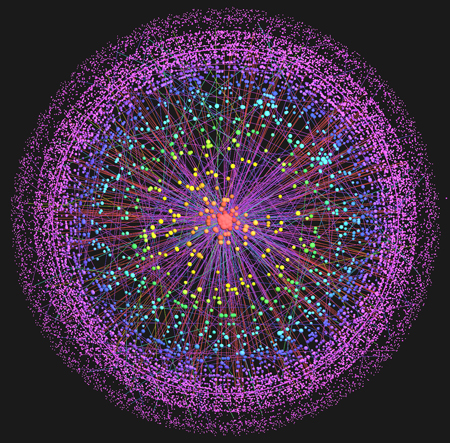
This is an interesting new approach to mapping the Internet Technology Review: Mapping the Internet. The work draws on the research project DIMES, and has some interesting interactive graphing tools, and a downloadable client to join in the mapping project.
It is interesting to compare this to the excellent work done at CAIDA, such as the AS-level topology maps of IPv6 and IPv4, using these tools (skitter probes, BGP table analysis, and ancillary tools).
Returning to the magazine article from Technology Review this extract gives a good flavour of the contents:
It's the first study to look at how the Internet is organized in terms of function, as well as how it's connected, says Shai Carmi, a physicist who took part in the research at the Bar Ilan University, in Israel. "This gives the most complete picture of the Internet available today," he says.
While efforts have been made previously to plot the topological structure in terms of the connections between Internet nodes--computer networks or Internet Service Providers that act as relay stations for carrying information about the Net--none have taken into account the role that these connections play. "Some nodes may not be as important as other nodes," says Carmi.
The researchers' results depict the Internet as consisting of a dense core of 80 or so critical nodes surrounded by an outer shell of 5,000 sparsely connected, isolated nodes that are very much dependent upon this core. Separating the core from the outer shell are approximately 15,000 peer-connected and self-sufficient nodes.
Take away the core, and an interesting thing happens: about 30 percent of the nodes from the outer shell become completely cut off. But the remaining 70 percent can continue communicating because the middle region has enough peer-connected nodes to bypass the core.
With the core connected, any node is able to communicate with any other node within about four links. "If the core is removed, it takes about seven or eight links," says Carmi. It's a slower trip, but the data still gets there. Carmi believes we should take advantage of these alternate pathways to try to stop the core of the Internet from clogging up. "It can improve the efficiency of the Internet because the core would be less congested," he says.
To build their map of the Internet, published in the latest issue of the Proceedings of the National Academy of Sciences, the researchers enlisted the assistance of 5,000 online volunteers who downloaded a program to help identify the connections between the 20,000 known nodes.
The closest I can find to a full academic paper on this, rather than the magazine style article linked above, seems to be based on slightly earlier work very similar to CAIDA's, is an AS level topology analysis (paper).
@MISC{carmi-2006, author = {Shai Carmi and Shlomo Havlin and Scott Kirkpatrick and Yuval Shavitt and Eran Shir}, title = {MEDUSA - New Model of Internet Topology Using k-shell Decomposition}, url = {http://www.citebase.org/abstract?id=oai:arXiv.org:cond-mat/0601240}, year = {2006} }Abstract
The k-shell decomposition of a random graph provides a different and more insightful separation of the roles of the different nodes in such a graph than does the usual analysis in terms of node degrees. We develop this approach in order to analyze the Internet's structure at a coarse level, that of the "Autonomous Systems" or ASes, the subnetworks out of which the Internet is assembled. We employ new data from DIMES (see this http URL), a distributed agent-based mapping effort which at present has attracted over 3800 volunteers running more than 7300 DIMES clients in over 85 countries. We combine this data with the AS graph information available from the RouteViews project at Univ. Oregon, and have obtained an Internet map with far more detail than any previous effort. The data suggests a new picture of the AS-graph structure, which distinguishes a relatively large, redundantly connected core of nearly 100 ASes and two components that flow data in and out from this core. One component is fractally interconnected through peer links; the second makes direct connections to the core only. The model which results has superficial similarities with and important differences from the "Jellyfish" structure proposed by Tauro et al., so we call it a "Medusa." We plan to use this picture as a framework for measuring and extrapolating changes in the Internet's physical structure. Our k-shell analysis may also be relevant for estimating the function of nodes in the "scale-free" graphs extracted from other naturally-occurring processes.
I am going to try and find out some more about this very interesting work, and I'll update this posting to reflect new information as I receive it.
Tweet Posted by mofoghlu at June 20, 2007 11:09 PM | TrackBack